「人工知能(AI)」と一緒によく出てくる単語として「機械学習」や「ディープラーニング」などがあります。それぞれが何を指し、どのような違いがあるのかなどについて簡単にまとめました。
各単語の関係について
上記の3単語のうち、一番最初に生まれたものが「人工知能」で、人工知能の実現のための技術の1つとして「機械学習」があり、機械学習の手法の1つに「ディープラーニング」があるといった関係です。
人工知能(AI)とは?
主に物事についての判断したり、学習したり、推測したりするような、人間の脳が行う知的な作業をコンピューターで再現するようなプログラムやシステムを指します。一般にAIという言葉を聞くとイメージしやすいのが、SF作品によく見られるロボットのような、さまざまな作業を人間に代わって行ってくれるような「汎用型のAI」ですが、現状ではまだまだ実現には遠い状態です。現在主流となっているものは、何か特定の物事に限定して、人間の代わりに判断を行ってくれるような「特化型のAI」です。こうした特化型のAIを作るにあたって様々な技術が開発されてきましたが、そのうちの有力なものが「機械学習」です。
機械学習とは?
人工知能を実現するための技術の1つで、大量のデータをコンピューターに入力して「学習」(入力されたデータをコンピューターが分解・整理して作った、コンピューターなりの判断基準となる計算式)させることで、コンピューターが自分で判断を行えるようにするものです。画像の自動認識や、文章の判別など、様々な分野で利用されています。
この「学習」の方法にも様々なものがあり、あらかじめ「正解」「不正解」の情報を人間が用意して、そのデータを基に判断基準を作成させる「教師あり学習」や、「正解」「不正解」のデータを渡さずに判断基準を作成させる「教師なし学習」などが有名です。
ディープラーニング(深層学習)とは?
機械学習の手法の1つで、複雑なデータを正しく処理できるように、判断基準となる計算式(層)を多数生成して、判断を行わせる手法です。原則として、学習を進めて判断の材料となる層が増えるほど、より精度の高い判断ができるようになります。コンピュータの処理能力の向上により、より多数の層を、より短時間で処理できるようになったため、様々な分野での活用が期待できます。
生産ラインの整流化を支援することに注力したライン整流化ソフト『NILE』を株式会社ウイルテック様を通じて発売しました。既存の工程分析ソフトウェアが複雑すぎて使いこなせないという声を元に、直感的な操作にこだわって開発しました。
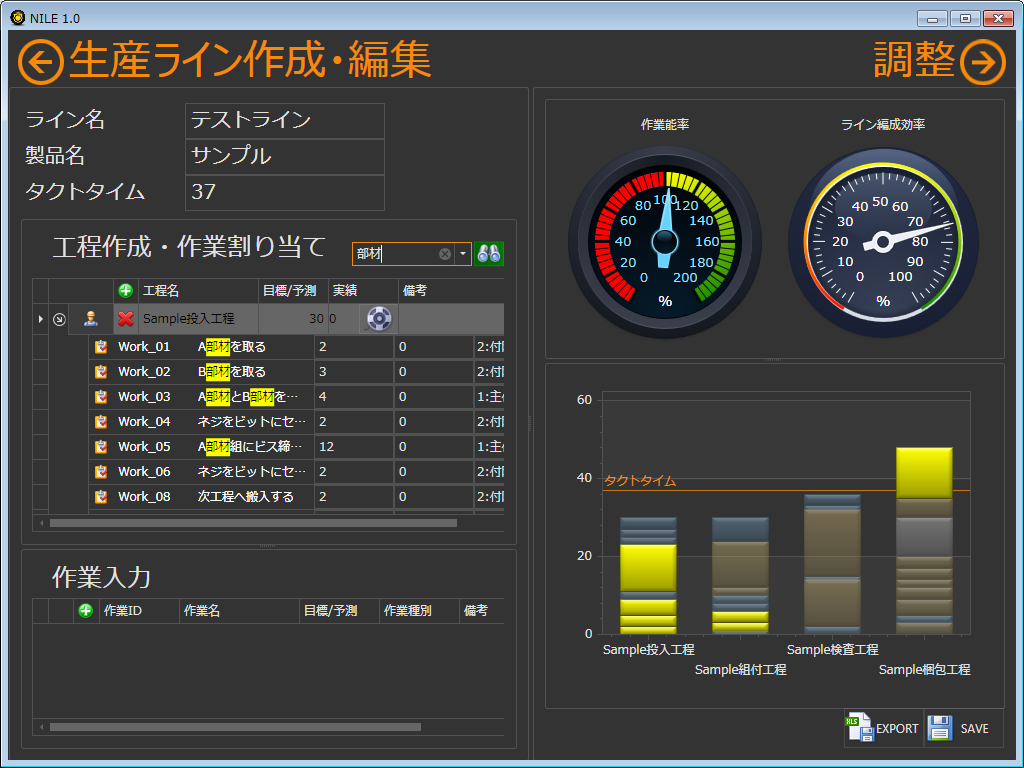
特徴1.「生産性の向上」に特化
各生産ラインの能力をグラフィカルに表現するメーターを搭載。作業効率、ライン編成効率をひと目で把握し、改善することが可能です。
作業工程の動画を取り込み、ワンタッチで単位作業へと分割・登録することができます。
特徴2.キーワード検索で簡単抽出
検索ボックスを利用すれば、膨大なデータの中から必要な情報だけをハイライト表示。編集の手を止めることなく、スムーズにラインの調整を行うことができます。
特徴3.狙い通りの工程編成を実現
作業全体の流れを分割して1つ1つの作業をブロックとして管理し、積み上げグラフに表示します。ブロックをドラッグ&ドロップするだけで簡単にラインを編成することが可能です。
詳細はこちらの専用サイトをご覧ください。
